統計学について

 

「アニマルサイエンス技術者は統計学者であるべきである」とはコーネル大学獣医学部のCheong准教授の言葉です。

言うまでもなく日本には優れた獣医・畜産学に関わる技術者がいて、そして優れた統計科学者がいます。

しかし、この２つの学問分野が連携して、研究・現場で応用されている例は、国内ではほとんど見受けられません。米国では、獣医・動物科学に関わる大学院生は統計学の習得が必須です。日本においても今後、酪農現場で統計学を意識した技術導入が進むことが、酪農科学のより深い理解と、海外の技術者と共通の言語で議論できることに繋がっていくと思われます。下記に海外の酪農学術誌で良く認められる統計用語を列挙します。

​

有意差

​

有意とは偶然によって差が生じる確率（p: probabilityの略）が非常に低い場合を指します（統計学の慣例として5%もしくは1%未満）。たとえば「p<0.05なら有意差あり」というのが一般的です。下表の例では試験区は酵母を給与、対照区は無給与として、試験区の乳量が増えた場合、統計計算したp値が0.02であれば偶然以外の要因（すなわち酵母給与）によって乳量が増えた確率は98%なので、有意差があると判断します。p値が0.20であれば80％の確率で偶然以外の要因で差が生じているが、偶然で差が生じる確率は20%で、5%より明らかに高く「有意ではない」ので酵母給与によって差が生じたとは言えないと解釈します。

​

 

​

​

​

​

 

​ANOVA

​

ANOVAとはanalysis of varianceの略で、日本語で「分散分析」と訳されます。分散分析とは２つ以上の要因が、ある結果に影響を与えていると考えられる場合に、各要因の影響が有意か有意でないかを分析していく手法を言います。一つしか要因が無ければt-検定という方法が使用出来ます。しかしながら、現場において「乳量が増えた」「繁殖が改善した」という結果に対して、たった一つの要因が影響する場合は多くありません。

下記に、ある乳牛の乳量がどのような要因（＝因子）で決定されるかの一例を示しています。因子としては国や地域などで普遍的な平均乳量、そして偶然よって生じる差である誤差が先ず挙げられます。さらに農場ごとの飼養管理の違いが農場差という因子となるかも知れません。産次数も要因となり得ます。添加物の酵母給与の有無が影響する可能性もあります。

​乳量を決めるこれらの因子を分離できたら、次に各因子が本当に影響を与えているかを分析します。それが分散分析となります。

​

​
 

​

​

​

​

分散分析は、各因子の影響が、誤差による影響より大きいか少ないかを調べます（下式）。有意に大きければ、「その因子は、偶然では無く、有意に乳量に影響を与えている」と判断できます。

 

​

​

​

​

分散分析で重要なのは、効果を因子で分解するという作業です。誤差の中に他の因子が隠れているかも知れないからです。誤差の中に他の因子が隠れていれば、結果（この場合は乳量）を左右する大事な要因を見落とすことに繋がったり、分散分析の精度自体が落ちたりしてしまいます。偶然（＝誤差）以外の因子を分離する思考過程は、現場で結果を改善させるために、或いは結果が予測より低い場合に、何が影響を与えているかを​分析することにも役立ちます。

​

共分散

​

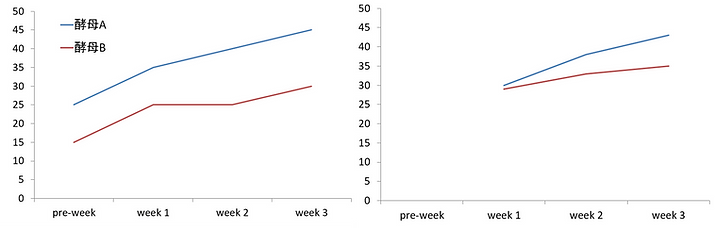
共分散はcovariateという単語でJournal of Dairy Scienceに頻出します。酪農現場で共分散を考慮に入れる意義としては「スタートラインを揃えること」と捉えておけば良いでしょう。下の左側グラフでは、酵母給与試験で酵母Aが酵母Bよりも乳量を増やしたことを示しています。しかしこのグラフでは、試験開始前のpre-week時点で既に差があり、本当に酵母Aによって乳量が増えたか判然としません。

そこでpre-week時の乳量が、その後の乳量に影響をあたえる因子となっているかを分析し、有意に影響を与えていれば因子として分離することで、結果判定の精度があがります。この場合、「pre-week時点での乳量」が共分散となります。共分散を因子として分離し、改めて酵母の分析を行ったのが右側グラフとなります。共分散を分離できていないと、各因子が過大もしくは過小評価されるリスクが高まります。

​

​

​

​

​

​

​

​

​

​

​

​

共分散構造

​

共分散構造はcovariate structureと英語で表記され、動物の経時試験を実施する際に考慮すべき因子の一つとなります。現場において、飼料原料を変えた、飼料設計をした、など新たな要因を加えた場合、経時的に評価するのは言うまでもありません。そして、日毎の乳量や週毎の乳成分の経時変化を評価していく場合、各時点における乳量・乳成分は時間的に前後無関係に独立しているとは言い切れません。現時点での結果は、前時点から影響を受け、次時点に影響を与えている可能性があるからです。

下図では、青線の各時点の乳量同士の相関性を点弧線で示しています。

​

​

​

​

​

​

​

 

 

 

 

 

別の表現をすれば、同じ個体は時間を経ても同じ生産能力を有し、今日時点で乳量が高い牛は、翌日も、翌々日も高乳量を維持する可能性があるので、日乳量と日乳量の間の相関性を分離評価する必要があります。その相関性を評価する方法が「共分散構造の確認」となります。共分散の項目で先述したように、相関性の有無を確認してモデルに取り入れれば、過小過大評価することなく、結果に影響する各因子の効果を判断できるようになります。

なお、共分散構造には多種類あり、対象となる経時変化に最も合致する共分散構造を選択するという方法がJournal of Dairy Scienceの論文で良く認められます。

​

サンプルサイズ​

​

試験区と対照区を評価するに当たり、考慮しなければいけない事項としてサンプルサイズがあります。ある因子を導入した場合、極端な例として試験区1頭、対照区1頭では、評価結果は信用できるか疑いが生じます。

統計評価の目的は、得られた試験結果が普遍的に受け入れられるか確認することです。国内の全ての牛を2分して試験区と対照区に分けるのは不可能ですので、その代わりに、代表ととなる牛をランダムに選んで（サンプリングして）、各区に割り当てて試験をして統計分析をすれば、偶然では無く効果があるのか確認できます。区に割り当てる頭数規模のことをサンプルサイズと言います。

有効とされるサンプルサイズは、因子による効果の大きさと、評価対象項目のバラツキ程度によって決定されます。例えば、新しい飼料原料を採用した場合、0.5㎏乳量が増えるのか、5㎏乳量が増えるのか、効果の大きさが違えば、必要とされるサンプルサイズは異なります。また、普遍的な乳量のバラツキは28～32㎏の間に収まるのか、それとも、20㎏～40㎏まで範囲が広がっているのか、ということによっても適切なサンプルサイズは変わってきます。

酪農科学における、参照サンプルサイズを下に示しましたが、統計処理の分析精度を上げるには、個々の因子によるサンプルサイズを計算した方が良いでしょう。また、現場においても、新しい技術・飼料を導入して評価するにあたり「この供試頭数では十分であるか」を考慮して試験を計画し、結果の考察を行えば、導入判断はしやすくなります。

​

​

​

​

​

​

​

​

​

​

標準誤差

​

酪農学術誌でSEもしくはSEMと表示される標準誤差はデータの読み取りに理解すべき項目の一つです。標準誤差は、普遍的な集団（統計学では母集団と表現されます）から繰り返しサンプリングし、そのサンプルの平均値を計算していくと、平均値がどれくらいばらつくかを現します。母集団の平均値の推定範囲とも捉えられますし、標準誤差が大きければ、ある因子による影響はばらつきが大きいとも解釈できます。

一方、標準偏差はSDと表現され、これは単にあるデータのばらつき度合を示しています。しかしながら、現場で有用な情報は「ある因子を国内の全ての牛に導入した場合にどのような平均値が得られて、その推定範囲はどれくらいであるか」であるので、平均値±標準誤差という論文データがあれば因子を導入する際の目安となり根拠となり得ます。

尚、グラフで各区の標準誤差のエラーバーを示す場合と（下図）、表で区の中で最大の標準誤差を示す場合があり（下表）、前者は区ごとのばらつきの確認、後者は評価項目そのもののばらつきの確認として読み取ります。

​

​

​

​

​